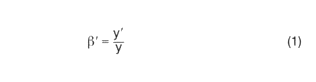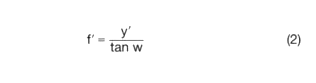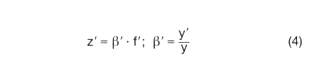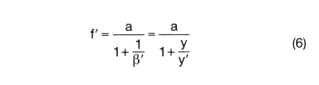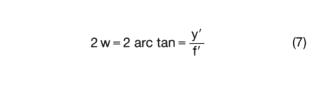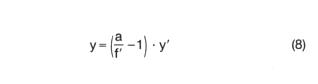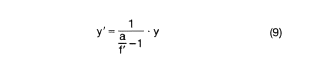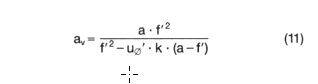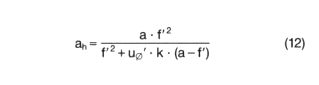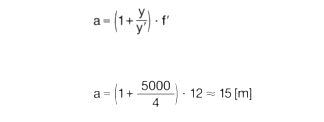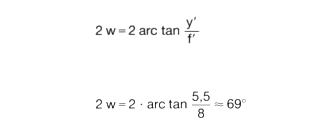Optical imaging
An object of size y located at a distance of the object distance a in front of the lens is imaged by the lens onto the image plane, which is located at a distance of the image distance a' behind the lens. There, the image sensor of the camera is located. The image size is y'. The change in image size depending on the object size is determined by the Image scale
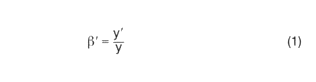
Image angle
The maximum extent of the object captured by the lens, starting from the reference plane of the lens, can be described by the image angle w. If the object is at infinity, the image is at the focal point F' of the lens. In this case, there is a simple relationship between the image angle w, the image size y', and the focal length f':
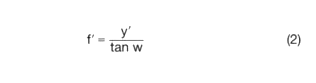
Aperture number
The aperture number k is a measure of the illumination intensity (image brightness). It depends on the focal length f' and the diameter of the entrance pupil ⌀EP, which represents the image of the aperture in the object space. Looking from the front into the lens, you see the diameter EP. Thus,

Extreme close-up
Lenses are designed for a specific range of object distances, usually from infinity to a certain minimum object distance (MOD). For possibly required shorter focusing distances, the possible displacement (stroke) of the lens from the image plane for focusing is no longer sufficient. Here, two options are available to capture very close objects, with a loss in imaging quality expected.
a) With the help of an extension tube, the distance between lens and image can be increased. The length of the extension tube z' is determined by the focal length f' and the magnification β' (lens in position ∞):
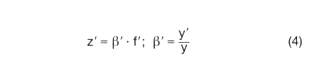
b) With the help of a close-up lens, the object distance can be shortened. When setting the lens to infinity (∞), an object distance a is obtained in front of the close-up lens, which corresponds to the focal length. The reciprocal of this required focal length (= required adjustment distance a) gives the required refractive power D of the close-up lens, which is given in diopters (dpt = 1/m):

User formulas
a Object distance = distance object-lens in mm (OH)
y Object size (half diagonal) in mm
y' Image size (half diagonal) in mm
for 1/2" format: 2 y' = 8 mm
for 2/3" format: 2 y' = 11 mm
for 1/A" format: 2 y' = 16 mm
β' Magnification = y'/y
Focal length
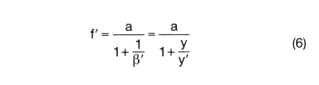
Image angle
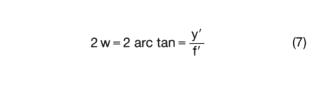
Object size
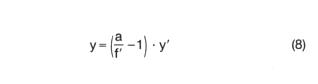
Image size
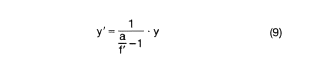
Object width

Depth of field (range)
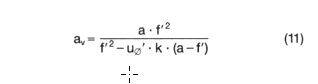
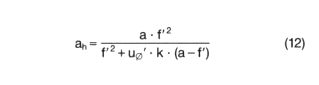
av Object width in front (in the direction of light) that is still sharply imaged
ah Object width in the rear (in the direction of light) that is still sharply imaged.
The range of object width between av and ah is referred to as depth of field.
u⌀' Diameter of blur circle to be defined depending on the application. For example, for the 2/3" format, u⌀' = 30 μm makes sense.
1.2 Calculation examples
(1) Given: Object size, distance, and sensor format;
Required: Focal length of the lens
An object of size y = 2.6 m at a distance a = 4 m should be fully captured with a 2/3" camera (2y ' = 11 mm). What focal length of the lens is required?
Formula (6):

(2) Given: Object size, sensor size, focal length
Required: Object distance
A 10 m large object (y = 5 m) should be fully captured with a 1/2" camera (y' = 4 mm) and a Schneider-Kreuznach 1.4/12 mm lens. How far must the camera be from the object?
Formula (10):
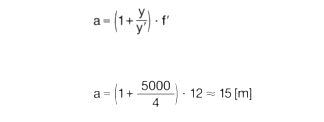
(3) Given: Focal length, sensor size
Required: Image angle w
What solid angle must a lighting illuminate to obtain a uniformly bright image with a 2/3 camera (2y' = 11 mm) and a Schneider-Kreuznach 1.4/8 mm lens?
Formula (7):
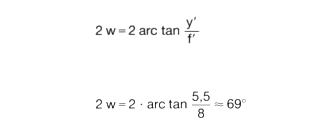
(4) Determination of object size for different image sensor formats (with the same lens)
Object distance 1/2 inch sensor: 2 y' = 8 mm
a = 1 m 2/3 inch sensor: 2 y ' = 11 mm
f' = 35 mm 1 inch sensorr: 2 y' = 16 mm
Formula (8):

So, the ratio of object sizes is equal to the ratio of sensor sizes.