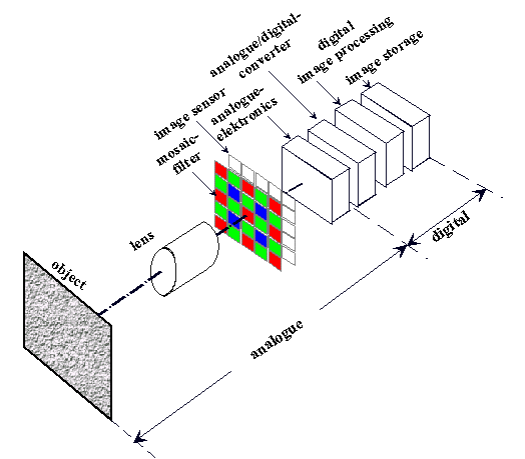
The transfer chain in digital photography
Digital photography Fig. 1: The transfer chain in digital photography
Image quality is affected by a whole series of links (components) in the apparatus used in the process of taking a picture (i.e., components of the digital camera). It is customary to speak of the transfer chain with its individual links (components), which can be classified as left.
Each link in this chain influences the image quality, either positively or negatively. This applies especially to the lens, since it stands at the beginning of this chain. What is lost at this stage can only be recovered with difficulty. The lens transfers the visual information of the object to be depicted onto the plane of the image sensor. In what follows, this process will be examined in detail in order to describe the different factors which have an influence on the image quality of the optical system.
Geometrically accurate reproduction
To answer this question, there are different features which have to be considered all together:
- image sharpness and contrast
- geometrically accurate reproduction
- brightness distribution over the image
- good light transmission by the lens
- a minimum of scattered light (stray light)
- absence of color fringes
We are going to examine these individual factors which influence image quality in this order.
Image sharpness and contrast
Of course you want to see the finest details of your subject appear absolutely sharp in the final image. To begin with, in order to be able to judge the reproduction of such details, a numerical measure for these fine details of definition has to be found. For this purpose, it is customary to use light/dark structures, i.e., a black/white test grid composed of equally wide light and dark bars. The resulting fineness of definition is expressed by the number of pairs of black/white bars per millimeter or, as it is usually stated, in the number of: line pairs per millimeter.
The next question which is immediately raised is the following: What details must be able to be seen before one can speak of a impeccably sharp final image? It is understandable that this depends on the enlargement of the digital image as it ultimately appears on the picture which is viewed.
In general, the image sensors of digital cameras are relatively small, and if one starts with final image of 10 x 14 cm in size, it follows that the enlargement factor may range from 20 to 30 times the size of the original. In general, one can assume that a picture can be regarded as impeccably sharp if, when viewed from a distance of 25 cm, it has a resolution of about 4 line pairs per millimeter.

Fig. 2: Test grid for determining the degree of definition of detail. The figure gives examples with increasing fineness of definition from left to right.
As far as the fineness of definition in the image of the lens (on the sensor) is concerned, this means that the optical system must be able to render details of definition of 80 to 120 line pairs per millimeter. However, this statement is not yet complete. It also depends on the degree of contrast which is reproduced between the light and dark bars in these structures. For the smaller the difference between the light and dark bars, the more difficult it is to recognize the details. The following figure will illustrate this.
From the bottom toward the top, the test grids show increasing contrast (in percent), and from left to right, increasing fineness of definition (in the number of line pairs per cm).
If you view this picture on a 17-inch monitor with a resolution of 1024 x 768 pixels from a distance of about 1.5 meters, the finest structures (in the picture on the right) would be equal to about 4 line pairs per mm. You will find that, at a low level of contrast, the finest structures are practically unrecognizable.
If one wants to describe the focusing capability of a lens, then one can draw a line from test figure to test figure with the respective contrast which the lens can reproduce for that test figure. This curved line is called the contrast transfer function (or MTF, Modulation Transfer Function).
In fig. 3, two such curves are drawn; here, the upper curved line stands for the qualitatively better lens, since it reproduces comparable details of definition with higher contrast (higher modulation). This is shown in graphic form in the following diagram (Fig4.).
The conclusion which we have reached in our consideration of image sharpness and contrast is thus: The highest possible contrast with the greatest possible fineness of definition (up to a reasonable upper limit; see above), distributed as evenly as possible over the entire image field.
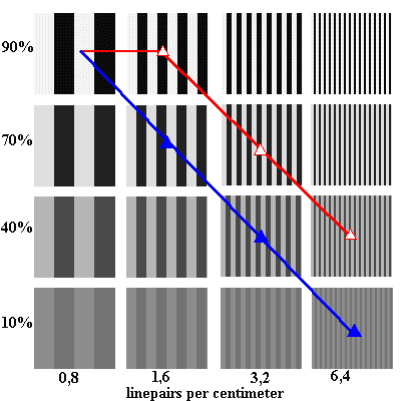
Fig. 3: Fineness of definition and contrast
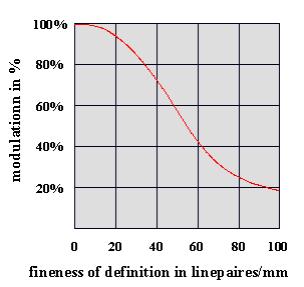
Fig. 4: The modulation transfer function (contrast!) as the function of fineness of definition (in line pairs per mm).
Geometrically accurate reproduction
This means that a geometrical figure (e.g., a circle, a square, a window frame, a door, etc.) is represented without distortion, and not, e.g., as an oval, pincushion-shaped, or barrel-shaped figure. In optics, if such a defect appears, it is called distortion. Distortion is described as the deviation of the distorted image point from its geometrically correct position, expressed in percent. In general, it increases more or less evenly from the center of the image to the image edge. Distortions of this are much more noticeable in regular objects, e.g., the facade of a house with windows, doors, etc., than in the case of irregular structures like pictures of landscapes. The distortion can be "pincushion-shaped" (positive) i.e., cause a stretching of the objects depicted, or "barrel-shaped" (negative), in which case the objects depicted appear to be compressed; see fig. 5. In actual practice, a distortion of less than 2% is no longer noticeable.
Fig. 5: Distortions in an actual object. From left to right: the original image; with a 10% pincushionshaped distortion; with a 10% barrel-shaped distortion
Brightness distribution over the image
The image produced by the lens should be evenly bright up to the edge of the image field. A light loss toward the edge of the image field is especially noticeable, and in the case of unstructured subjects like the sky, water, sand, etc., can be quite annoying. A light loss is expressed as the proportion of brightness at the edge of the image field to the brightness at the center of the image (in percent) in an evenly bright object. In the field of optics, one speaks of the relative irradiance of the lens. Fig. 6 shows examples for different degrees of light loss toward the edge of the image field. The corners of the image are the darkest, since they are the farthest from the center of the image. Particularly in the case of wide-angle lenses, a certain amount of light loss is, for reasons having to do with physics, unavoidable. As the figures show, a light loss of 25% does not have a disturbing effect.

Fig. 6: Examples of light loss at the image edge
Good light transmission by the lens
(spectral transmission)
The capability of making good pictures, even at low levels of illumination, is assured by the high speed of the lens, which is described by reference to the aperture ratio (e.g., 1:3.5) or f-stop number k (e.g., k = 3.5). The lower the f-stop number k is, the faster the lens. This f-stop number, however, does not take into account the reduction of the light as it passes through the elements of the lens. This light loss results from absorption (reduction) in the lens elements, and because of reflections at the air/glass interfaces, and is dependent on the color (wave length) of the entering light. Good light transmission (spectral transmission) is achieved only with high-quality optical lens elements and with very good coating (elimination of reflections) at the surfaces of the lens elements, using numerous extremely thin systems of layers applied by an evaporation process. The spectral transmission is expressed in percent in dependence of the color of the light (wave length). Fig. 7 shows an example.
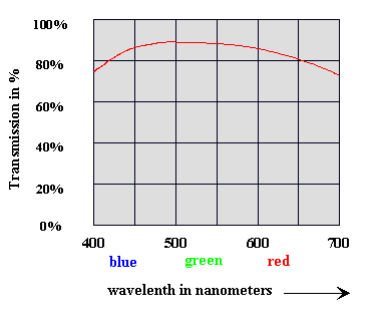
Fig. 7: Spectral transmission
Minimum levels of scattered light (stray light)
Stray light manifests itself as a uniform brightness level which is superimposed on the image (useful light). This is caused by undesired reflections at the lens mountings, the diaphragm blades, and the lens surfaces, and causes the dark parts of the image to appear brighter. The dynamic range, i.e., the ratio of the brightest to the darkest point on the image is thereby reduced, and of course the contrast in the finer details as well. Good lens systems have a stray light ratio of less than 3 %. Fig. 8 shows, as an example, the object (upper left), and then stray light ratios of 6%, 12%, and 24%.

Fig. 8 Various stray light ratios in a picture. From upper left to lower right: original image, 6%, 12%, and 24%.
Absence of color fringes
Color fringes occur along light/dark or dark/light edges, and take the form of a colored seam or line along those edges. We have already become acquainted with such light/dark transitions as test patterns: they are the black/white bar grids of fig. 2. These are reduced in the process of taking a picture, not only in their contrast, but they also show colored lines as well. In this connection, it is not only the expansion of the colored lines which is of significance, but also the question as to how brilliant or pale the colors are. Color fringes are an especially critical factor in digital photography.
The opto-electronic image sensor (cf. fig. 1) consists of regularly arranged square image elements which are called pixels (from the English phrase "picture element"). Unlike traditional photography using colored film, where the light-sensitive elements consist of irregularly formed granular structures, the color fringes at the transitions along the edges are especially noticeable in the regular pixel structure.
Fig. 9 shows a simulation of color fringes for two real lenses, where the upper example is significantly weaker with regard to color fringes than the lower one.
The illustration shows how the color fringes arise in the image plane (i.e., on the surface of the image sensor) by means of the lens. Here, the text grid structure (i.e., every black or white bar) has an extension of 1 pixel, 2 pixels, and 4 pixels (from left to right). The usual pixel size for digital cameras lies between 2.8 and 3.5 µm, i.e., 2.8 and 3.5 thousandths of a millimeter! For a pixel size of 3 µm, this means details of definition of 160, 80, and 40 line pairs per millimeter.
To be sure, the image sensor "sees" the colors differently: in so doing, each pixel averages the brightness and color across its light-sensitive surface. As a result, each pixel has a uniform color and a uniform brightness, as fig. 10 shows. Color fringes can arise, not only in the optical system, but also in other links of the transfer chain (cf. fig.1), e.g., through the mosaic filter of the image sensor and in connection with digital image processing (digital color interpolation).
Good color correction is achieved in the optical system when the the color fringes have an expansion of less than 2 pixels with relatively little color saturation.

Fig. 9 Color fringes on black/white test grids for two real lenses
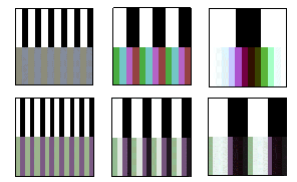
Fig. 10 This is the way the image sensor "sees" the color fringes
Final remarks
We have shown that there are many factors which determine the "good image quality" of a lens. A balanced evaluation of the totality of these parameters is thus required in order to be able to properly assess the imaging quality of a lens. A further point, which could not be discussed in this introduction, also has to do with the regular pixel structure of the image sensor, one which is responsible, among other things, for the occurrence of color fringe structures: It is the so-called cross-talk effect or (in English) aliasing.