The human eye can only see, approximately, wave-lengths between 0.400 μm (blue) and 0.700 μm (red). All those wavelengths combined appear to us to be white light, such as the natural light we see outdoors. Most, if not all, commercial off-the-shelf (COTS, also called “standard catalog”) lenses are optically designed to create a high-quality image using white light.
However, while machine vision light sources exist that can create close-to-nature white light, many users do not use white light sources in their applications. As a result, digital camera-based vison system users can experience problems related to the responsivity of digital sensors to discrete wavelengths, including those produced by lasers and LEDs. A critical element of avoiding such issues is properly defining lighting requirements early in systems engineering when designing a vision system. Just as important, if white light is not being employed in the application, system designers and end users should understand the problems they might encounter, as well as how to identify and resolve those problems before the impact on their imagery is too late to correct.
Case Examples
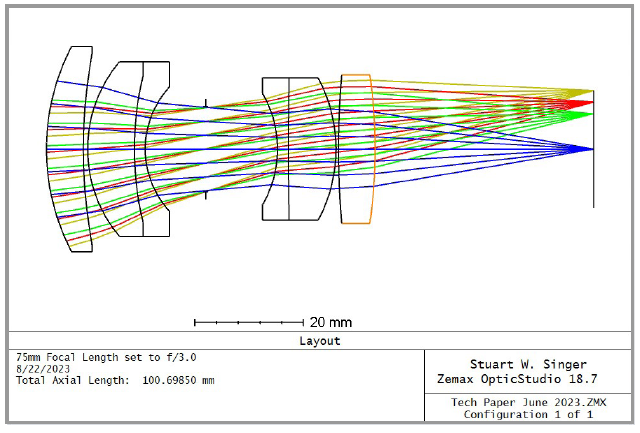
When a lens is designed, the number of individual wavelengths that can be considered within the design is limited. A weight factor for each specific wavelength that considers the digital sensor’s responsivity also fac-tors into design. Numerous resources covering how to choose individual wavelengths and weighting factors are available in print and online. For purposes of this discus-sion, we will use a 75 mm focal length lens set to f-Stop = f/3.0 as an example (Fig. 1).
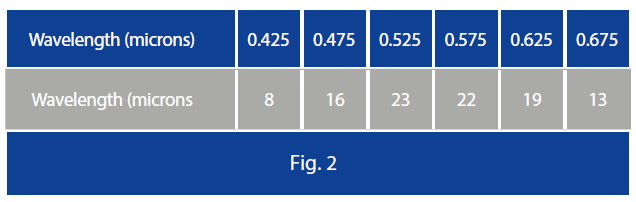
Depending on the design software used by the lens creator(s), anywhere from a single wavelength to ap-proximately 10 wavelengths can be assessed as part of the design. We find, for white light COTS lenses, six wavelengths — along with weighting factors for each wavelength — typically are sufficient. The following wavelengths and weight have been used for purposes of this example (Fig. 2).
Next, we completed the lens design for a sensor/camera containing 5 μm2 pixels. This pixel size limits maximum resolution to 100 line pairs per millimeter (commonly ex-pressed as Lp/mm and referred to as the Nyquist limit). One of our previous articles — Math, Magic And MTF: A Cheat Sheet For The Vision System Community — dis-cusses how to convert pixel size into Nyquist Lp/mm and how to read and understand a modulation transfer func-tion (MTF) plot. The article notes that, by looking at the MTF values at 67% of the Nyquist value (in this case, 67 Lp/mm), the aim would be to create a lens with all MTF values > 30%. The 75 mm f/3.0 lens depicted above was finished to the following MTF performance (Fig. 3).
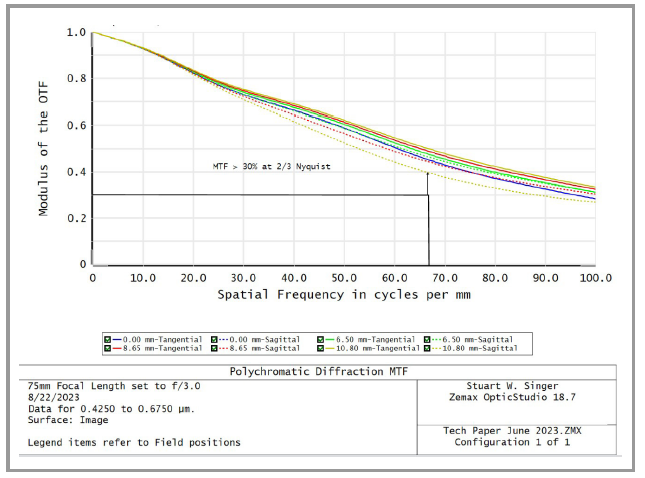
Fig. 3 - MTF plot calculated using the values expressed in Fig. 2.
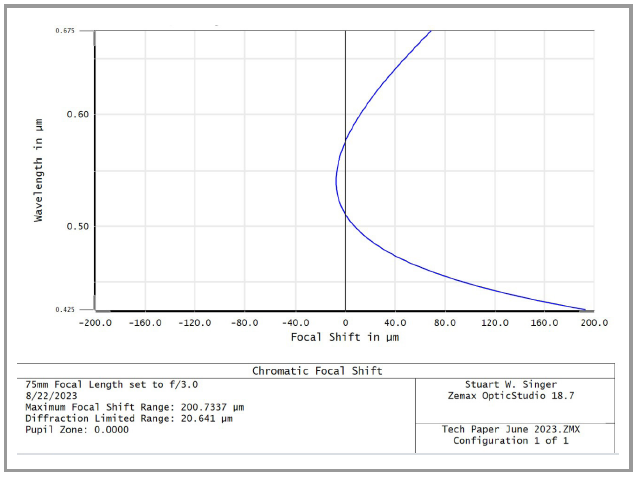
Fig. 4
As depicted in Fig. 3, at 67 Lp/mm, all on- and off-axis MTF values are > 30%, confirming for the end user that the lens functions very well for a COTS unit. The MTF lens performance is a calculated value showing the best overall focus position for visible white light.
Notably, a chromatic focus shift plot (also called an axial chromatic focus plot) is a valuable piece of lens design performance data not typically made available to end users unless they request it. Still, the chromatic focus shift plot — which shows how the lens shifts focus along the optical axis, with respect to wavelength, for peak performance — can be calculated easily (Fig. 4).
But what happens when your optical system does not require white light as an illumination source, using instead one or more monochromatic wavelengths sources (e.g., from lasers and/or LEDs)? Consider the same example above, but with the lens kept at best visible white light focus using only one monochromatic wavelength: 0.425 μm (Fig. 5).
Note how, when keeping focus at best visible light and then changing the illumination to a monochromatic source (Fig. 5), the MTF lines drop precipitously well before the 67 Lp/mm value on the plot. In fact, the lens essentially dies and falls below 30% MTF around the 30 Lp/mm value. Once the MTF lines hit zero on the X axis (horizontal), they recover and rise, but this is considered spurious resolution that contains a phase shift and cannot be used.
In short, in this scenario, the user no longer has any optical performance data that is usable . However, by changing the focus of the lens by the magnitude and direction depicted in the chromatic focus shift plot above (Fig. 4), the user regains lost performance — or generates superior MTF values compared to the white light MTF plot (Fig. 6).
Now, consider the use of more than one monochromatic illumination source. The user would have to keep changing the lens’ focus settings depending upon which monochromatic sources were being used.
In many systems, this approach is impractical, but a number of solutions exist:
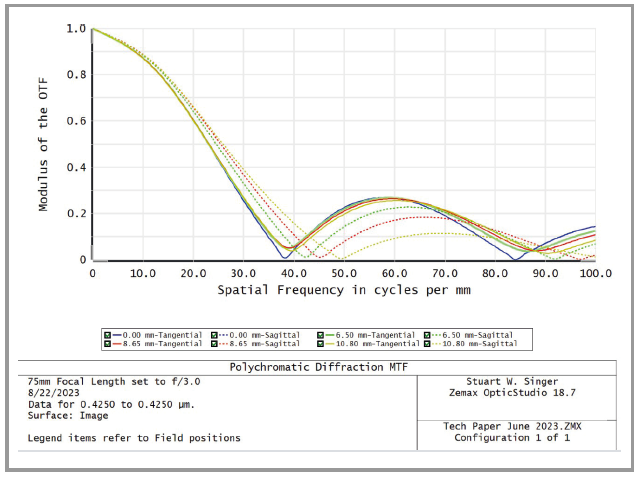
Fig. 5

Fig. 6
1. Purchase or produce a customized lens design, specifying the exact monochromatic illumination wavelengths for the design engineers to implement. This usually is a costly approach, and it can take a lot of time to obtain a working prototype lens for testing. Still, if the user intends to apply, for example, three different monochromatic illumination sources, the lens design can be optimized such that the lens would not require refocusing when switching between those sources.
2. It is necessary to manually adjust focus for each wavelength, unless the user purchases or produces a motorized focus lens. By combining chromatic focus shift plot values and some lab-based empirical testing, the user could optimize the magnitude and direction the focus must shift to send accurate signals to the focus shift motor.
3. The user could employ a liquid focus shifting lens (also called a variable focus liquid lens) in combination with a COTS lens. By recording their own focus shift values with respect to the monochromatic wavelength sources being employed, the user can arrive at the values the liquid focus lens will require to shift to the optimized focus position.
Lastly, users could discover, through empirical lab testing, a compromise in focus. Their system might be able to function just well enough — with much lower MTF performance values — to provide sufficient resolution for the application. Obviously, this is not an ideal solution, more of a final option if the above paths are unavailable. Every lens, from any manufacturer, will perform differently with respect to this wavelength focus shift. 4 Fig. 5 Fig. 6
Final Thoughts
Regardless of the lens manufacturer, purchasing a visible corrected lens with the intent to use monochromatic, dis-crete wavelength sources can lead to trouble well into the design and development of an imaging system — if proper steps are not taken to understand the elements that impact lens performance across different applications.