Bild 2: Objektseitig telezentrisches Objektiv
O1, O2 - Prüflingspositionen,
1 - Hauptstrahl
B1 - Sensorposition,
B2 - Bildebene für Prüflingsposition O2
Es wurde von zwei Prüflingspositionen O1 und O2 ausgegangen. Von der Position O1 aus wird der Prüfling in die Sensorebene B1 scharf abgebildet. Befindet sich der Prüfling in O2 erfolgt die scharfe Abbildung nach B2. In B1 entsteht ein verschwommenes Bild des Prüflings, welches aber formal gesehen die gleiche Größe aufweist, wie bei der Abbildung von O1 aus. Zu dieser Größenkonstanz kommt es, weil der Hauptstrahl objektseitig telezentrisch, d.h. parallel zur optischen Achse, verläuft. Die Art und Weise, wie es zu dem verschwommenen Bild in B1 kommt ist aber unsymmetrisch. Man sieht in Bild 2 sehr gut, daß das Lichtbündel, welches in B1 das Bild von O2 erzeugt, unsymmetrisch ist. Der obere Bündelteil beleuchtet ein größeres Gebiet von B1 als der untere. In der Realität kann man die Auswirkungen dieses Effektes bereits bei Defokussierungen von einigen zehntel Millimetern beobachten.

Bild 3: Kantenbilder eines Objektivs ohne bildseitige Telezentrie
exakt fokussiert und um -0.3 mm defokussiert radial - tangential
Bild 3 zeigt die Kantenbildfunktion zu einem Objektiv, das bei korrekter Fokussierung keinerlei Unsymmetrie aufweist (1. Darstellung). Wird um -0.3 mm defokussiert, wird das tangentiale Kantenbild unsymmetrisch. Den gleichen Effekt beobachtet man auch bei einer Defokussierung um +0.3 mm. Obendrein stellt man eine Drift des Kantenortes in tangentialer Richtung fest. Berücksichtigt man in diesem Beispiel beide Effekte, so muß mit einer Unsicherheit von bis zu 4 µm bei der Detektion der tangentialen Kante gerechnet werden. Wenn man bedenkt, daß eine Detektionsgenauigkeit von 1 µm durchaus möglich ist und bei optimaler Beleuchtung sogar noch unterschritten werden kann, so bedeutet diese Unsicherheit eine signifikante Beeinträchtigung der Meßgenauigkeit. Ähnliche Ungenauigkeiten entstehen auch wenn der Sensor uneben ist bzw. nicht senkrecht zur optischen Achse steht.
3. Vorteile der beidseitigen Telezentrie
Die oben beschriebenen Effekte der Symmetrieänderung des Kantenbildes bei Defokussierung bewirken eine deutliche Verschlechterung der Meßgenauigkeit. Sie können vermieden werden, wenn das verwendete Meßobjektiv nicht nur objektseitig, sondern auch bildseitig telezentrisch ausgelegt wurde. Bild 4 zeigt die Grundprinzipien der Abbildung mit solch einem Objektiv.
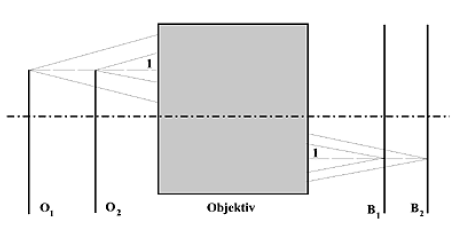
Bild 4: Beidseitig telezentrisches Objektiv
O1O2 - Prüflingspositionen, 1 - Hauptstrahl
B1 - Sensorposition,
B2 - Bildebene für Prüflingsposition O2
Dabei entspricht die Abbildungssituation der aus Bild 2, d.h. O1 wird in die Sensorebene B1 scharf abgebildet und von O2 entsteht in B1 ein unscharfes Bild. Der wesentliche Unterschied zu Bild 2 besteht in der bildseitigen Telezentrie, dem achsparallelen Verlauf des Hauptstrahls 1 im Bildraum. Wegen dieser Telezentrie im Bildraum erfolgt die Verwaschung des Bildes von O2 in B1 symmetrisch, denn das Schnittbild von B1 mit dem dargestellten Lichtbündel ist kreisförmig. Folglich bleibt das Kantenbild trotz Defokussierung symmetrisch und die Kante kann exakt detektiert werden. Im Resultat kann man beim Einsatz beidseitig telezentrischer Objektive davon ausgehen, daß die theoretisch mögliche Detektionsgenauigkeit erreichbar ist, wenn Beleuchtungssituation und Kantenstruktur optimal sind.
4. Beidseitig telezentrische Messobjektive von Schneider-Kreuznach
Wegen der ständig steigenden Anforderungen an die Genauigkeit von berührungslosen Meßsystemen haben wir uns entschlossen, eine Reihe von beidseitig telezentrischen Meßobjektiven auf den Markt zu bringen. Die Reihe umfaßt fünf Objektive mit den Abbildungsmaßstäben 1:1 bis 1:5. Neben dem entscheidenden Merkmal der beidseitigen Telezentrie weisen diese Objektive folgende zusätzliche Merkmale auf:
- Die Lichtstärke wurde im Vergleich zu den derzeit am Markt verfügbaren Objektiven deutlich erhöht. Die numerische Apertur beträgt 0.14 bzw. 0.13.
- Die Objektive sind in einem Bereich von 3 mm bildseitig fokussierbar. Auf der Objektseite kann man deshalb den Arbeitsabstand variabel gestalten. Die Grenzen hierfür sind allerdings vom Abbildungsmaßstab abhängig. Die Arbeitsbereiche für die fünf Objektive mit den Abbildungsmaßstäben 1:1, 1:2, 1:3, 1:4 und 1:5 sind 6 mm, 24 mm, 54 mm, 96 mm und 150 mm groß. Der Abbildungsmaßstab bleibt beim Umfokussieren konstant.
- Die Objektive weisen eine sehr geringe Verzeichnung auf. Mit einer entsprechenden Kalibrierung kann leicht Verzeichnungsfreiheit erreicht werden.
5. Zusammenfassung
Fehlende bildseitige Telezentrie bei Meßobjektiven bewirkt bei Defokussierung unsymmetrische Kantenbilder bzw. deren Drift. Das führt zu einer ungenauen Kantendetektion, so daß die theoretisch mögliche Genauigkeit deutlich verfehlt wird. Beidseitig telezentrische Objektive weisen diese Schwächen nicht auf und ermöglichen somit eine erfolgreiche Annäherung an die mögliche Meßgenauigkeit.

SYLVINE telezentrisches Objektiv


 (1)
(1)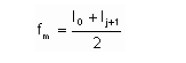 (2)
(2)



